I used the Sagarin ratings to get information on the teams' expected performance.
The difference between the ratings for two teams is the expected spread and I used the normal distribution with a standard deviation of 8.83 points to get the probability of a team beating another team.
I then simulate the whole tournament as many times as I like using a random number generator and the probability generated above to pick the winner of each matchup.
To make my picks I then compared a particular set of picks to the simulations, typically 1000, to determine the points for that set of picks.
Recall that in the bracket pool in which I participate not only are the rounds weighted 1,2,4,8,16,32 for rounds 1 through 6, but you multiply those points by the seed of the winning team. If Utah State makes it to the final four, for that round you get 8 points times its 12 seed or 96 points.
I compared several selections to each other to try to find the one that had the most points in competition with other selections in my simulations.
Top seed advances wins - 6% of simulations
Top Sagarin points advances wins - 23% of simulations
Top Pomeroy rating advances wins - 25% of simulations
Secret winning picks wins - 47% of simulations
Thus I was at least able to find a set of picks that outperformed Sagarin and Pomeroy in my simulations. I suspect it has something to do with the seed rating. The results reflect the expected outcomes before the start of the tournament but after the play-in games.
A chart (click for larger) showing the expected outcome of a given seed helps explain why lower seeds might yield more potential points than higher seeds. using the simulated results, the top plot shows the expected round that a team will advance to. Round 6 is the championship. The middle plot shows the expected points for a given seed assuming a standard point scheme of 1,2,4,8,16, and 32 points for winning a round. The bottom plot is the one of interest here, it includes the seed rating in the points.
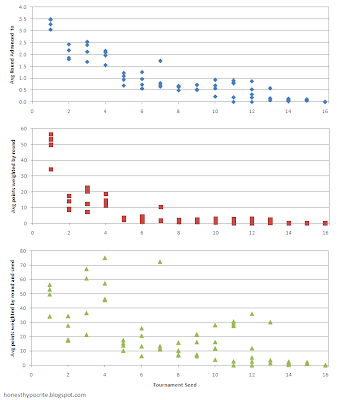 Upper plot: First seeds are expected to do well advancing to the elite eight on average. Next seeds two through four generally make it to the sweet sixteen. Seeds from about 5 through twelve generally make it one round, and that uncertainty is where the fun comes in.
Upper plot: First seeds are expected to do well advancing to the elite eight on average. Next seeds two through four generally make it to the sweet sixteen. Seeds from about 5 through twelve generally make it one round, and that uncertainty is where the fun comes in.Middle plot: The standard point assignments don't change the expected value of a team much.
Bottom plot: Including the seeds in the expected points really shows how three and four seeds can be worth much more than a one seed. Even more interestingly, the correct 10 through 13th seed can be worth more points than a five through 9 seed, because they do about as well in the tournament, but have more points due to the seed multiplier. That is what makes the seed multiplier a fun bracket pool game.
No comments:
Post a Comment